「NOIP 模拟赛」大

题目大意：滑稽树上滑稽果，滑稽树下你和我，滑稽树前做游戏，滑稽多又多。树上有 $n$ 个节点，它们构成了一棵树，每个节点都有一个滑稽值 $a_i$，每次你可以选择一个最大滑稽值和最小滑稽值不超过 $d$ 的连通块并把它们删掉，请问你最少能用几次把这些节点都删掉？$n,d,a_i \leq 5000$

我们可以设 $f[i][j][k]$ 表示使得以 $i$ 为根的连通块的最大值为 $j$ 最小值为 $k$ 的最少步数，这样的DP是 $O(n^3)$ 的。

考虑在数轴上以每个 $a_i$ 为左端点画一个长度为 $d$ 的区间，如图

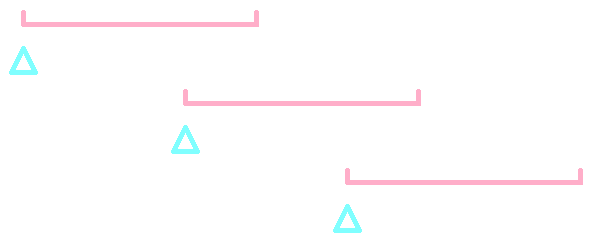
那么只有区间有交集的节点才可以同时选择。

考虑每个区间的意义，它表示每个节点所在连通块的最大值的取值范围，相当于化简了DP数组的最小值那一维。

设 $f[i][j]$ 表示使得以 $i$ 为根的连通块的最大值为 $j$ 的最小步数，$g[i]$ 表示删除子树 $i$ 的最小步数。

DP转移方程见代码。

#include <cstdio>
#include <cstring>

const int N = 5005;
int n, d, a[N], f[N][N], g[N], head[N], nxt[N<<1], v[N<<1], tot;

int min(int x, int y) {
    return x < y ? x : y;
}
void add_edge(int from, int to) {
    nxt[++tot] = head[from];
    head[from] = tot, v[tot] = to;
}
void dfs(int u, int fa) {
    for (int i = a[u]; i <= a[u] + d && i <= 5000; ++i)
        f[u][i] = 0;
    for (int i = head[u]; i; i = nxt[i]) {
        if (v[i] == fa) continue;
        dfs(v[i], u);
        for (int j = a[u]; j <= a[u] + d && j <= 5000; ++j)
            f[u][j] += min(g[v[i]], f[v[i]][j]);
    }
    for (int i = a[u]; i <= a[u] + d && i <= 5000; ++i)
        g[u] = min(g[u], f[u][i] + 1);
}

int main() {
    freopen("big.in", "r", stdin);
    freopen("big.out", "w", stdout);

    scanf("%d%d", &d, &n);
    memset(f, 0x3f, sizeof f);
    memset(g, 0x3f, sizeof g);
    for (int i = 1; i <= n; ++i) scanf("%d", &a[i]);
    for (int i = 1, u, v; i < n; ++i) {
        scanf("%d%d", &u, &v);
        add_edge(u, v), add_edge(v, u);
    }
    dfs(1, 0);
    printf("%d\n", g[1]);

    fclose(stdin);
    fclose(stdout);
    return 0;
}

时间复杂度 $O(n^2)$