题目大意:在一个长为 $L$ 的坐标轴上,有 $M$ 个分布不均的石子,有一只青蛙要从 $0$ 跳到 $L$,每次跳跃距离的范围是 $[S,T]$,问最少踩到多少枚石子?$S,T \leq 10, M \leq 100, L \leq 10^9$
由于 $M$ 很小,可以进行路径压缩。
根据「NOIP 2017」小凯的疑惑可知,如果 $n \perp m$,则最大的不能由 $n$ 和 $m$ 累加来表示的数为 $n \times m-(n+m)$,于是我们可以用 $t$ 和 $t-1$ 来转移,下图为 $t=4$ 的情况:
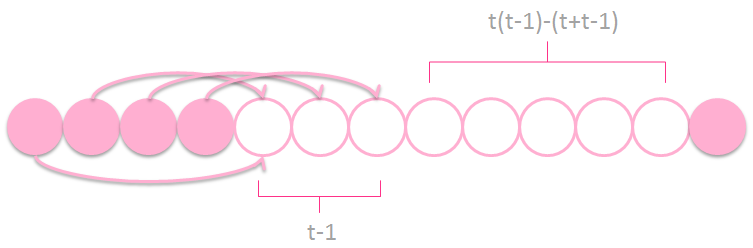
我们可以越过 $t(t-1)-(t+t-1)$ 的区域到达一个每个位置都可及的空位区($t-1$),通过这个空位区可以转移到左边的每一个可以一步跳到的石子。
如果两石子间的距离大于 $t-1+t(t-1)-t-t+1=(t-2)t$,把它变为 $(t-2)t$ 即可。
实现需要注意以下几点:
- 注意特判 $s=t$ 的情况
- $t=2$ 时 $(t-2)t=0$,但应该把间距控制成 $1$ 而不是 $0$,因为中间一定要留一个空位区
- 不要忘记排序
- 到达终点或越过终点都可以
#include <cstdio>
#include <algorithm>
#include <cstring>
int a[105], b[100005], f[100005];
int read() {
int x = 0; char c = getchar();
while (c < '0' || c > '9') c = getchar();
while (c >= '0' && c <= '9') {
x = (x << 3) + (x << 1) + (c ^ 48);
c = getchar();
}
return x;
}
int min(int x, int y) {
return x < y ? x : y;
}
int main() {
int l = read(), s = read(), t = read(), m = read();
for (int i = 1; i <= m; ++i) a[i] = read();
if (s == t) {
int ans = 0;
for (int i = 1; i <= m; ++i)
if (a[i] % t == 0) ++ans;
printf("%d\n", ans);
} else {
int n = 0, lim = t * (t - 2);
if (lim == 0) ++lim; //注意特判t=2的情况, 中间一定要留一个空位
std::sort(a + 1, a + m + 1); //不要忘记排序
for (int i = 1; i <= m; ++i) {
int d = a[i] - a[i-1] - 1;
if (d > lim) d = lim;
n += d + 1, b[n] = 1;
}
if (l - a[m] - 1 > lim) l = n + lim + 1;
else l = n + l - a[m];
memset(f, 0x3f, sizeof f);
f[0] = 0;
for (int i = s; i <= l; ++i) {
for (int j = i - t; j <= i - s; ++j) {
if (j < 0) continue;
f[i] = min(f[i], f[j]);
}
if (b[i]) ++f[i];
}
for (int i = l - t; i <= l; ++i) { //可以越过终点
if (i < 0) continue;
f[l] = min(f[l], f[i]);
}
printf("%d\n", f[l]);
}
return 0;
}
时间复杂度 $O(n \log n)$