题目大意:给定一个 $n \times m$ 的棋盘,上面放有 $nm-1$ 个棋子,有些棋子不能移动,有些棋子可以移动,$q$ 次给出 $E_i,E_j,S_i,S_j,T_i,T_j$,分别表示空白格子的位置,并请你求出把 $(S_i,S_j)$ 上的棋子移动到 $(T_i,T_j)$ 的最少步数。$1 \leq n,m \leq 30, q \leq 500$
直接暴力 $bfs$ 有 $30$ 分,但可以发现,两个状态不同当且仅当目标棋子的位置或空白格子的位置不同,设当前目标棋子的位置为 $(x_1,y_1)$,空白格子的位置为 $(x_2,y_2)$,那么我们用 $(x_1,y_1,x_2,y_2)$ 来表示当前状态,其他棋子的位置无所谓。由于 $(x_1,y_1)$ 和 $(x_2,y_2)$ 的各有 $nm$ 种,因此总的状态数是 $(nm)^2$,时间复杂度 $O(q(nm)^2)$,期望得分 $60$。
如图为目标棋子从 $(3,2)$ 转移到 $(2,3)$ 的过程:

这个过程可以分为如下几段:
- 把空白格子从初始位置移动到目标棋子的上/下/左/右
- 交换空白格子与目标棋子,转移到 $(3)$
- 把空白格子移动到与目标棋子四连通的其他 $3$ 个位置,转移到 $(2)$
于是可以把每个格子 $(i,j)$ 拆成四个点,分别表示当目标棋子在这个格子时,空白格子在 $(i-1,j),(i+1,j),(i,j-1),(i,j+1)$ 的状态。
然后在这三个步骤之间连边,对于 $(1)(3)$ 的边权可以预处理出两个格子的最短距离,$(2)$ 的边权就是 $1$。
预处理两个格子的最短距离时,因为边权都是 $1$,所以可以直接 $O(n^2)$ bfs。
还需要注意的是,并非预处理任意两个格子的最短距离,应该是在不移动目标棋子的条件下,任意两个与其四连通的棋子的最短距离,如下图:
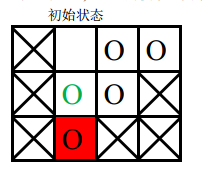
如果我们处理的是任意两个格子的最短距离,会把直接 $(1,2)$ 移动到 $(3, 2)$,然后把 $(2,2)$ 与 $(3,2)$ 交换,但这样是不可能实现的,因此要加上不移动目标棋子的条件。
由于每次询问只会更改目标棋子和空白格子的位置,因此不用每次重新建图,只需更改空白格子的起点到目标棋子上/下/左/右的四条连边即可。
这样的点数最多是 $4nm$,边数最多是 $16nm$,可以用 $Dijkstra$。
注意特判起点与终点重合的情况。
#include <cstdio>
#include <cstring>
#include <queue>
const int INF = 0x3f3f3f3f;
const int dx[4] = {-1, 0, 0, 1};
const int dy[4] = {0, -1, 1, 0};
struct Node {
int x, y;
} a[1000];
struct Edge {
int to, cost;
} e[20000];
struct Pair {
int x, y;
bool operator < (const Pair &rhs) const {
return x > rhs.x;
}
};
std::priority_queue<Pair> Q;
int id[35][35], dis[1000][5][5], f[4000], cnt, n, m;
int head[4000], nxt[20000], tot, S, T;
int read() {
int x = 0; char c = getchar();
while (c < '0' || c > '9') c = getchar();
while (c >= '0' && c <= '9') {
x = (x << 3) + (x << 1) + (c ^ 48);
c = getchar();
}
return x;
}
int check(int x1, int y1, int x2, int y2) { //判断两点是否为四连通
for (int i = 0; i < 4; ++i)
if (x1 + dx[i] == x2 && y1 + dy[i] == y2) return i;
return -1;
}
void bfs(int p, int s, int ids) { //预处理在不移动目标棋子的条件下, 任意两个与其四连通的格子的距离
int vis[1000] = {}, d[1000] = {}, q[1000] = {}, head = 0, tail = 0;
q[tail++] = ids, dis[p][s][s] = 0, vis[ids] = 1;
while (head < tail) {
int x = a[q[head]].x, y = a[q[head]].y;
for (int i = 0; i < 4; ++i) {
int xx = x + dx[i], yy = y + dy[i];
if (xx && xx <= n && yy && yy <= m && id[xx][yy] && id[xx][yy] != p && !vis[id[xx][yy]]) {
q[tail] = id[xx][yy], d[tail] = d[head] + 1, vis[id[xx][yy]] = 1;
int t = check(a[p].x, a[p].y, xx, yy);
if (t != -1) dis[p][s][t] = d[tail];
++tail;
}
}
++head;
}
}
int bfs2(int p, int x1, int y1, int x2, int y2) { //在不移动目标棋子p的条件下, (x1,y1)到达(x2,y2)的最短路径
if (x1 == x2 && y1 == y2) return 0; //不要忘记判断x1=x2,y1=y2的情况
int vis[1000] = {}, d[1000] = {}, q[1000] = {}, head = 0, tail = 0;
q[tail++] = id[x1][y1], vis[id[x1][y1]] = 1;
while (head < tail) {
int x = a[q[head]].x, y = a[q[head]].y;
for (int i = 0; i < 4; ++i) {
int xx = x + dx[i], yy = y + dy[i];
if (xx == x2 && yy == y2) return d[head] + 1;
if (xx && xx <= n && yy && yy <= m && id[xx][yy] && id[xx][yy] != p && !vis[id[xx][yy]])
q[tail] = id[xx][yy], d[tail++] = d[head] + 1, vis[id[xx][yy]] = 1;
}
++head;
}
return INF;
}
void add_edge(int u, int v, int w) {
nxt[++tot] = head[u];
head[u] = tot;
e[tot] = (Edge){v, w};
}
void build() { //建最短路的图
for (int i = 1; i <= cnt; ++i) { //目标棋子的位置
for (int j = 0; j < 4; ++j) { //空白格子的位置
int x = a[i].x + dx[j], y = a[i].y + dy[j];
if (!x || x > n || !y || y > m || !id[x][y]) continue;
add_edge(i + j * cnt, id[x][y] + (3 - j) * cnt, 1); //空白格子与目标棋子交换
for (int k = 0; k < 4; ++k) { //与其他三个方向连边
if (j == k) continue;
int xx = a[i].x + dx[k], yy = a[i].y + dy[k];
if (!x || x > n || !y || y > m || !id[x][y]) continue;
add_edge(i + j * cnt, i + k * cnt, dis[i][j][k]);
}
}
}
}
void dijkstra() {
int vis[4000] = {};
Q.push((Pair){0, S});
memset(f, 0x3f, sizeof f);
f[S] = 0;
while (!Q.empty()) {
int u = Q.top().y;
Q.pop();
if (vis[u]) continue;
vis[u] = 1;
for (int i = head[u]; i; i = nxt[i])
if (f[u] + e[i].cost < f[e[i].to]) {
f[e[i].to] = f[u] + e[i].cost;
Q.push((Pair){f[e[i].to], e[i].to});
}
}
}
int main() {
n = read(), m = read(); int q = read();
for (int i = 1; i <= n; ++i)
for (int j = 1; j <= m; ++j)
if (read()) id[i][j] = ++cnt, a[cnt] = (Node){i, j};
memset(dis, 0x3f, sizeof dis);
for (int i = 1; i <= cnt; ++i) //目标棋子的位置
for (int j = 0; j < 4; ++j) //空白格子的位置
if (a[i].x + dx[j] && a[i].x + dx[j] <= n && a[i].y + dy[j]
&& a[i].y + dy[j] <= m && id[a[i].x+dx[j]][a[i].y+dy[j]])
bfs(i, j, id[a[i].x+dx[j]][a[i].y+dy[j]]);
build();
S = 1 + 4 * cnt, T = 2 + 4 * cnt;
while (q--) {
int ex = read(), ey = read();
int sx = read(), sy = read();
int tx = read(), ty = read();
if (sx == tx && sy == ty) { //特判起点与终点重合的情况
puts("0"); continue;
}
int tmp[3605] = {tot};
for (int i = 1; i <= 4 * cnt; ++i) tmp[i] = head[i];
for (int i = 0; i < 4; ++i) { //建起点与终点发出的边
int x = sx + dx[i], y = sy + dy[i];
if (x && x <= n && y && y <= m && id[x][y])
add_edge(S, id[sx][sy] + i * cnt, bfs2(id[sx][sy], ex, ey, x, y));
x = tx + dx[i], y = ty + dy[i];
if (x && x <= n && y && y <= m && id[x][y])
add_edge(id[tx][ty] + i * cnt, T, 0);
}
dijkstra();
if (f[T] < INF) printf("%d\n", f[T]);
else puts("-1");
tot = tmp[0]; //还原
memset(head, 0, sizeof head);
for (int i = 1; i <= 4 * cnt; ++i) head[i] = tmp[i];
}
return 0;
}
时间复杂度 $O(q \times 20nm\log(4nm))$